Chapter 7 Gráfico de controle para atributos
Ao relembrarmos o assunto distribuição de probabilidades de variáveis aleatórias discretas, podemos associar a terminologia “dados de atributo” a duas situações em específico:
Se cada item produzido é uma realização de uma variável aleatória e, se esta tem somente duas possibilidades, ou seja, é defeiuoso ou não defeituoso, então lembremos da distribuição bernoulli se fixarmos em um único item ou da distribuição binomial se fixarmos \(n\) itens.
Se cada item produzido pode ter um ou mais tipos de defeitos então lembremos da distribuição poisson que modela a contagem de defeitos de tal item.
Obviamente que para cada tipo de situação teremos um gráfico em específico.
7.1 Gráfico p para a fração de defeituosos
Consideremos uma amostra de tamanho \(n\) e seja \(X\) nossa variável aleatória que representa o número de itens defeituosos. Então o valor estimado da proporção de defeituos é \(\hat{p}=X/n\). Relembrando que se \(X\) tem distribuição binomail então \(E(X)=np\) e \(V(X)=np(1-p)\). Portanto,
\[ E(\hat{p}) = p \qquad V(\hat{p}) = \frac{p(1-p)}{n} \]
Pelo teorema central do limite sabemos que \(\hat{p}\) tem distribuição aproximadamente normal. Então, os limites inferiores e superiores do gráfico são os intervalos de confiança do parâmetro \(p\) ou \(\pi\) (como visto na disciplina de probabilidade e estatística).
Logo os limites de inferior e superior são
\[ LCI = p - 3\sqrt{\frac{p(1-p)}{n}} \qquad LCS = p + 3\sqrt{\frac{p(1-p)}{n}} \]
Se \(p\) for não conhecido, então precisamos estimá-lo como uma média das proporções calculadas nos \(t\) dias de amostragem, ou seja,
\[ \bar{p} = \frac{\sum_{i=1}^{t}\hat{p_i}}{t} \]
Novamente se \(LCI \le 0\) então substitua por zero.
7.1.1 Aplicação
Uma amostra de 100 xícaras de um determinado conjunto de jantar foi selecionada em 25 dias sucessivos, e cada uma foi examinada em busca de defeitos (https://lec.pro.br/download/R/dados/Devore_Ex16_6.xlsx.). Os números resultantes de xícaras defeituosos e as proporções amostrais correspondentes são os seguintes:
ex4 <- read.xlsx('Devore_Ex16_6.xlsx')
knitr::kable(ex4)| dia | ndefeitos |
|---|---|
| 1 | 7 |
| 2 | 4 |
| 3 | 3 |
| 4 | 6 |
| 5 | 4 |
| 6 | 9 |
| 7 | 6 |
| 8 | 7 |
| 9 | 5 |
| 10 | 3 |
| 11 | 7 |
| 12 | 8 |
| 13 | 4 |
| 14 | 6 |
| 15 | 2 |
| 16 | 9 |
| 17 | 7 |
| 18 | 6 |
| 19 | 7 |
| 20 | 11 |
| 21 | 6 |
| 22 | 7 |
| 23 | 4 |
| 24 | 8 |
| 25 | 6 |
No R temos,
# lendo os dados e vendo o resumo
ex4 <- read.xlsx('Devore_Ex16_6.xlsx')
summary(ex4)## dia ndefeitos
## Min. : 1 Min. : 2.00
## 1st Qu.: 7 1st Qu.: 4.00
## Median :13 Median : 6.00
## Mean :13 Mean : 6.08
## 3rd Qu.:19 3rd Qu.: 7.00
## Max. :25 Max. :11.00# calculando a proporção
prop = ex4[,2]/100
prop## [1] 0.07 0.04 0.03 0.06 0.04 0.09 0.06 0.07 0.05 0.03 0.07 0.08 0.04
## [14] 0.06 0.02 0.09 0.07 0.06 0.07 0.11 0.06 0.07 0.04 0.08 0.06# calculando a proporção média
pbarra = mean(prop)
pbarra## [1] 0.0608# calculando os limites
LCI = pbarra - 3*sqrt(pbarra*(1-pbarra)/100)
LCI #valor negativo## [1] -0.01088893LCI = 0
LCS = pbarra + 3*sqrt(pbarra*(1-pbarra)/100)
LCS## [1] 0.1324889Por fim o gráfico,
#plotando o gráfico
plot(prop, pch=16, type='b', xlab='Dia', ylab='Proporções', ylim=c(0,0.15),axes=FALSE)
axis(1,at=1:25)#inserindo o eixo x
axis(2)#inserindo o eixo y
abline(h = LCI, col='red')#colocando o LCI
abline(h = LCS, col='red')#colocando o LCS
abline(h = pbarra, col='blue')#colocando a média de controle 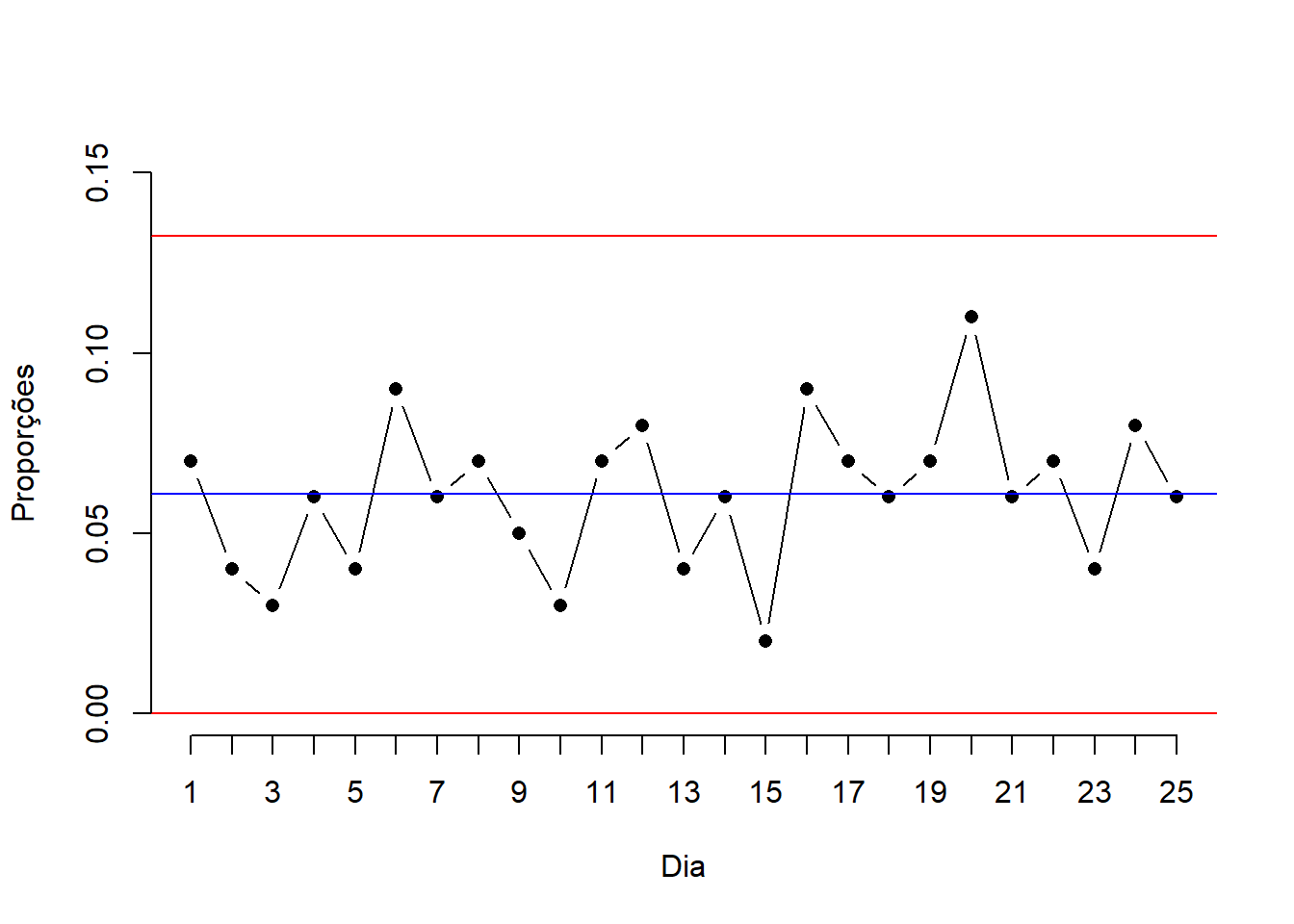
Utilizando o pacote qcc temos,
# colocando os dados de modo que o pacote entenda
qp = qcc(ex4[,2], sizes=rep(100,25), type='p') 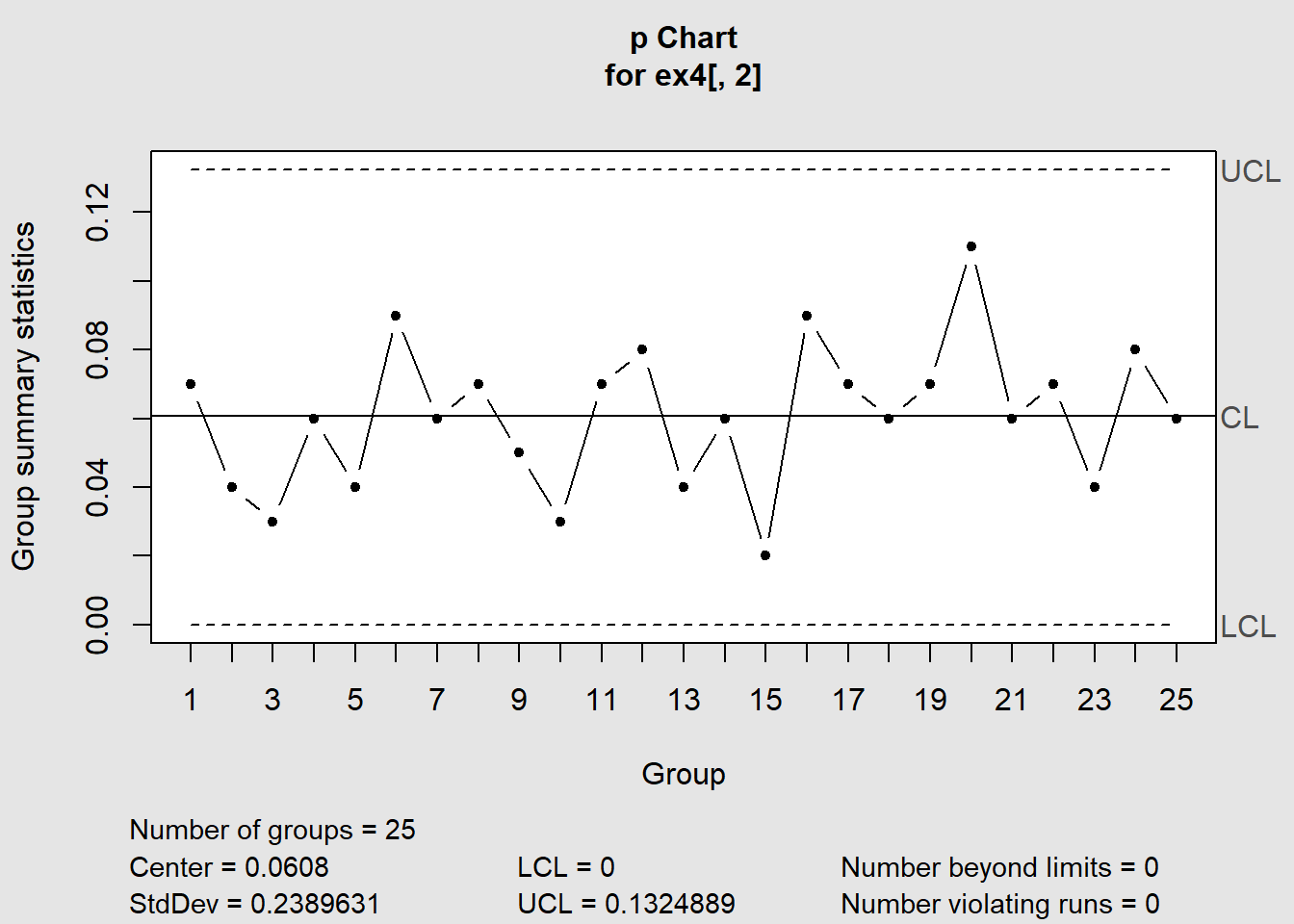
7.2 O gráfico c para o número de defeitos
Vamos focar agora no número de defeitos em um item, como por exemplo, na fabricação de brinquedos podemos observar em um brinquedo específico problemas como arranhões, pinturas incorretas, pedaços de fragmentos, montagem inadequada entre outros ou podemos considerar também um grupo de itens como por exemplo, rasgos em um conjunto de quatro pneus. No último caso, o tamanho do grupo é, por hipótese, o mesmo em cada instante do tempo.
Conforme já mencionado, o gráfico de controle para o número de defeitos se baseia na distribuição Poisson que, conforme já vimos os parâmetros são:
\[ E(Y) = \mu \qquad V(Y) = \mu \qquad \sigma_Y = \sqrt{\mu} \]
Seja \(\mu\) o parâmetro da Poisson para o número de defeitos em uma unidade então o cálculo para os limites inferior e superior é:
\[ LCI = \mu - 3\sqrt{mu} LCS = \mu + 3\sqrt{mu} \]
Se \(\mu\) for desconhecido então pode utilizar o estimador \(\bar{X}\).
7.2.1 Aplicação
Uma companhia produz painéis de metal que são conformados após terem sido inicialmente revestidos com uma mistura contendo cerâmica em pó (https://lec.pro.br/download/R/dados/Devore_Ex16_7.xlsx.). Algumas vezes aparecem defeitos na finalização destes painéis e a companhia deseja estabelecer um gráfico de controle para o número de defeitos. O número de defeitos em cada um dos 24 painéis amostrados em intervalos de tempos iguais são como:
ex5 = read.xlsx('Devore_Ex16_7.xlsx')
knitr::kable(ex5)| tempo | contagem |
|---|---|
| 1 | 7 |
| 2 | 10 |
| 3 | 9 |
| 4 | 12 |
| 5 | 13 |
| 6 | 6 |
| 7 | 13 |
| 8 | 7 |
| 9 | 5 |
| 10 | 11 |
| 11 | 8 |
| 12 | 10 |
| 13 | 13 |
| 14 | 9 |
| 15 | 21 |
| 16 | 10 |
| 17 | 6 |
| 18 | 8 |
| 19 | 3 |
| 20 | 12 |
| 21 | 7 |
| 22 | 11 |
| 23 | 14 |
| 24 | 10 |
No R temos,
xbarra = mean(ex5[,2])
LCI = xbarra - 3*sqrt(xbarra)
LCI## [1] 0.404175LCS = xbarra + 3*sqrt(xbarra)
LCS## [1] 19.17916Fazendo o gráfico no R,
#plotando o gráfico
plot(ex5[,2], pch=16, type='b', xlab='Dia', ylab='Nº de defeitos', ylim=c(0,25),axes=FALSE)
axis(1,at=1:25)#inserindo o eixo x
axis(2)#inserindo o eixo y
abline(h = LCI, col='red')#colocando o LCI
abline(h = LCS, col='red')#colocando o LCS
abline(h = xbarra, col='blue')#colocando a média de controle 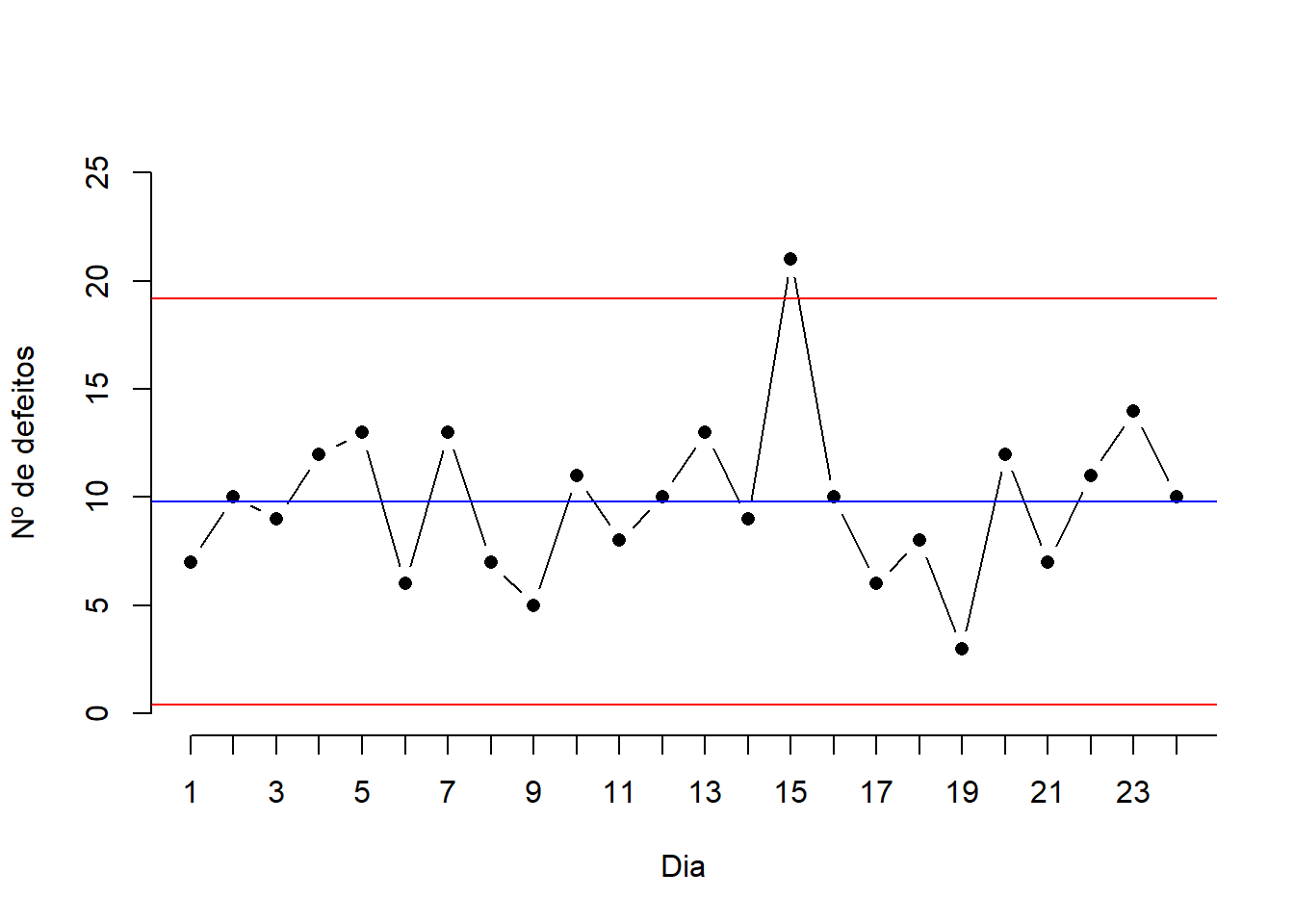
Utilizando o pacote qcc tem-se,
qn = qcc(ex5[,2], type='c') 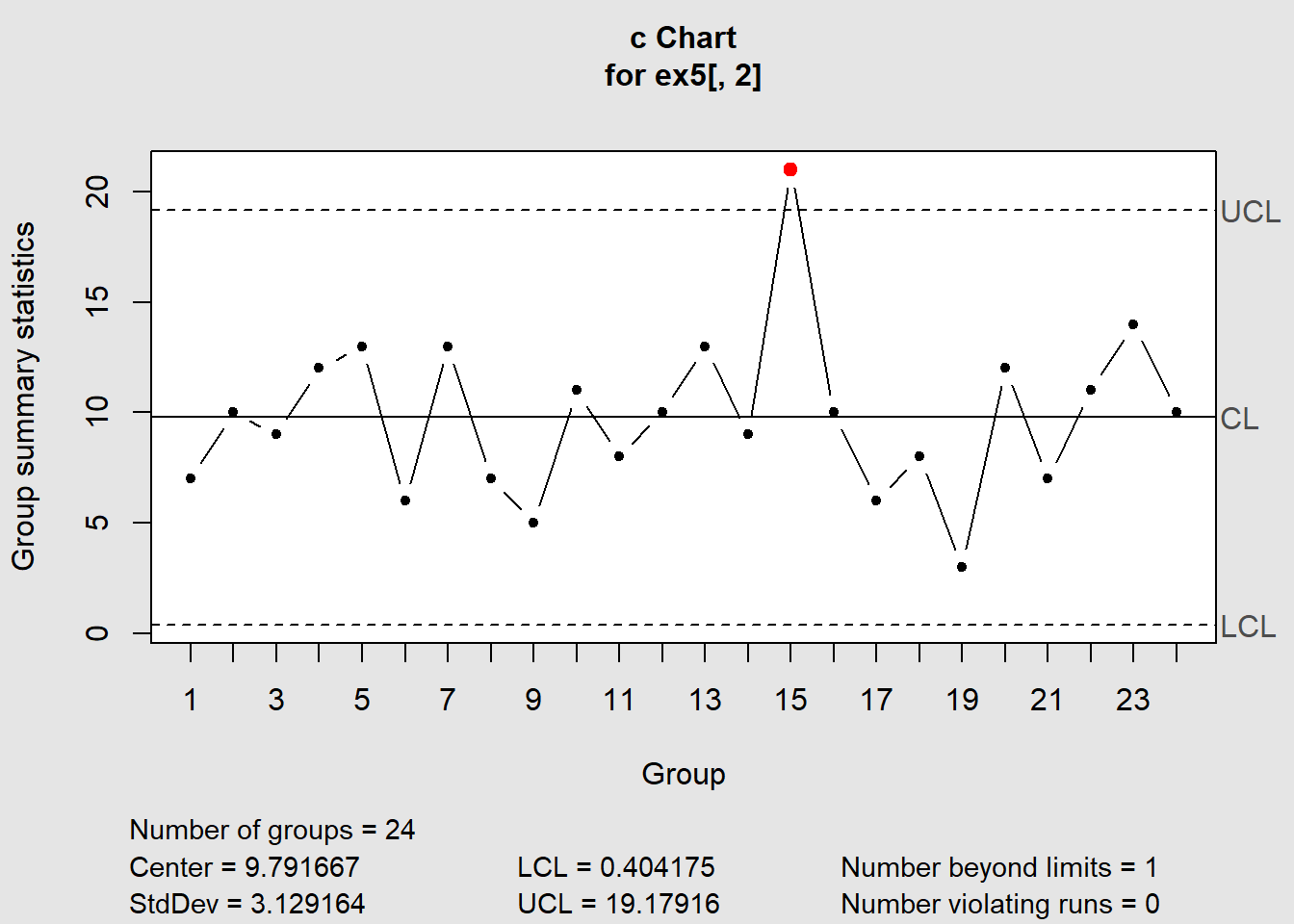
Verificou-se que houve um ponto acima do LCS. Após investigações descobriu-se que o item (painel) possuia um revestimento com viscosidade excepcionalmente baixa.