Chapter 6 Gráficos de controle para variações do processo
Já foi discutido na disciplina de probabilidade e estatística que as medidas de tendência central (ou localização) não descrevem por si só um conjunto de dados. Necessitamos também de uma medida que nos informe o quão dispersos estão os dados em relação a sua tendência. Em em processo de produção conseguimos perceber bem a importância das medidas de dispersão, pois queremos produzir algo com baixa variabilidade. Imagine que a produção de uma certa peça automotiva é extremamente cara e, que a variação em 3mm resulte em descarte da peça. Perceba que não basta produzirmos peças com uma média de 50mm por exemplo (supondo que este valor seja o ideal), pois se a variabilidade não estiver dentro de 3mm isto resultará em descarte da peça.
Vamos ver numericamente esta raciocínio. Considere em uma situação A que cinco amostras de tamanho 3 produziram as seguintes médias: 53; 51; 41; 55; 52. Calculando a média tem-se 50,4. Seja uma amostra B com cinco médias também provenientes de amostras de tamanho 3: 51; 49,9; 49; 51,1; 51. Calculando a média tem-se também 50,4. Sem fazer nenhum cálculo, é nítido que embora as situações produzam a mesma média, a situação B bem é bem mais estável do que a situação A.
Entendido a importância de se controlar as variações em um processo, será abordado neste material o gráfico S, que é o mais utilizado e o gráfico R, que embora esteja cada vez mais em desuso, alguns ainda o utilizam por uma questão de tradição.
6.1 O gráfico S
Consideremos novamente a retirada de \(t\) amostras aleatórias e independentes provenientes de uma variável aleatória com distribuição normal. Nestas amostras ao invés de estimarmos \(\bar{X}\) vamos estimar o desvio padrão, ou seja, \(S\). É natural que a estimativa da média dos desvios padrões das \(t\) amostras seja \(\bar{S} = \sum S_{i}/t\). Este valor será a reta central do gráfico. Precimos então determinar os limites inferior e superior do gráfico.
Retomando aos conceitos já aprendidos em probabilidade e estatística, a variância de qualquer variável aleatória \(Y\) é \(V(Y)=E(Y^2) - [E(Y)]^2\) e que a variância amostral \(S^2\) é um estimador não viciado de \(\sigma^2\), ou seja, \(E(S^2) = \sigma^2\). Como visto nos tópicos anteriores, a \(E(S) = a_n \sigma\). Então,
\[ V(S) = E(S^2) - [E(S)]^2 = \sigma^2 - (a_n \sigma)^2 = \sigma^2(1 - a_{n}^{2}) \]
A expressão de $a_n} já foi abordada no tópico de gráficos de localização. O desvio padrão é a raiz quadrada da variância, ou seja,
\[ \sigma_S = \sqrt{V(S)} = \sigma \sqrt{1 - a_{n}^{2}} \]
Podemos estimar \(\sigma\) como \(\hat{\sigma} = \bar{S}/a_n\). Portanto, podemos estabelecer os limites 3-sigma como:
\[ LCI = \bar{S} - \frac{3\bar{S}\sqrt{1 - a_{n}^2}}{a_n} \qquad LCS = \bar{S} + \frac{3\bar{S}\sqrt{1 - a_{n}^2}}{a_n} \]
Atente-se que para \(n \le 5\) o valor de \(LCI\) será negativo. Neste caso, utilize \(LCI=0\).
6.1.1 Aplicação
Os dados a seguir (https://lec.pro.br/download/R/dados/Devore_Ex43.xlsx.) são observações da resistência à tensão de amostras de tecido sintético selecionados de um processo de produção a intervalos de tempo iguais. Construa o gráfico S de controle e faça as devidas conclusões.
Utilizando o R temos:
ex3 <- read.xlsx("Devore_Exer43.xlsx")
summary(ex3) ## dia amostra resistencia
## Min. : 1.0 Min. :1 Min. :48.40
## 1st Qu.: 6.0 1st Qu.:1 1st Qu.:49.60
## Median :11.5 Median :2 Median :50.00
## Mean :11.5 Mean :2 Mean :50.18
## 3rd Qu.:17.0 3rd Qu.:3 3rd Qu.:50.70
## Max. :22.0 Max. :3 Max. :54.10# calculando o desvio padrão de cada dia
desviospadrao <- with(ex3, tapply(resistencia,dia,sd))
desviospadrao## 1 2 3 4 5 6 7
## 1.1718931 0.8544004 1.1357817 1.0969655 0.6658328 0.8544004 0.4163332
## 8 9 10 11 12 13 14
## 0.9643651 1.1590226 0.4725816 0.4932883 0.8326664 0.8386497 0.4041452
## 15 16 17 18 19 20 21
## 0.2645751 0.8544004 0.7810250 0.9018500 0.6429101 0.7937254 2.9308702
## 22
## 0.9712535# calculando a média dos desvio padrão
sbarra = mean(desviospadrao)
sbarra## [1] 0.8864062# calculando os limites inferiores e superiores
LCI = sbarra - (3*sbarra*sqrt(1-an(3)^2))/an(3)
LCI # vejam que é menor do que zero## [1] -0.503629LCI = 0
LCS = sbarra + (3*sbarra*sqrt(1-an(3)^2))/an(3)
LCS## [1] 2.276441Fazendo o gráfico,
#plotando o gráfico
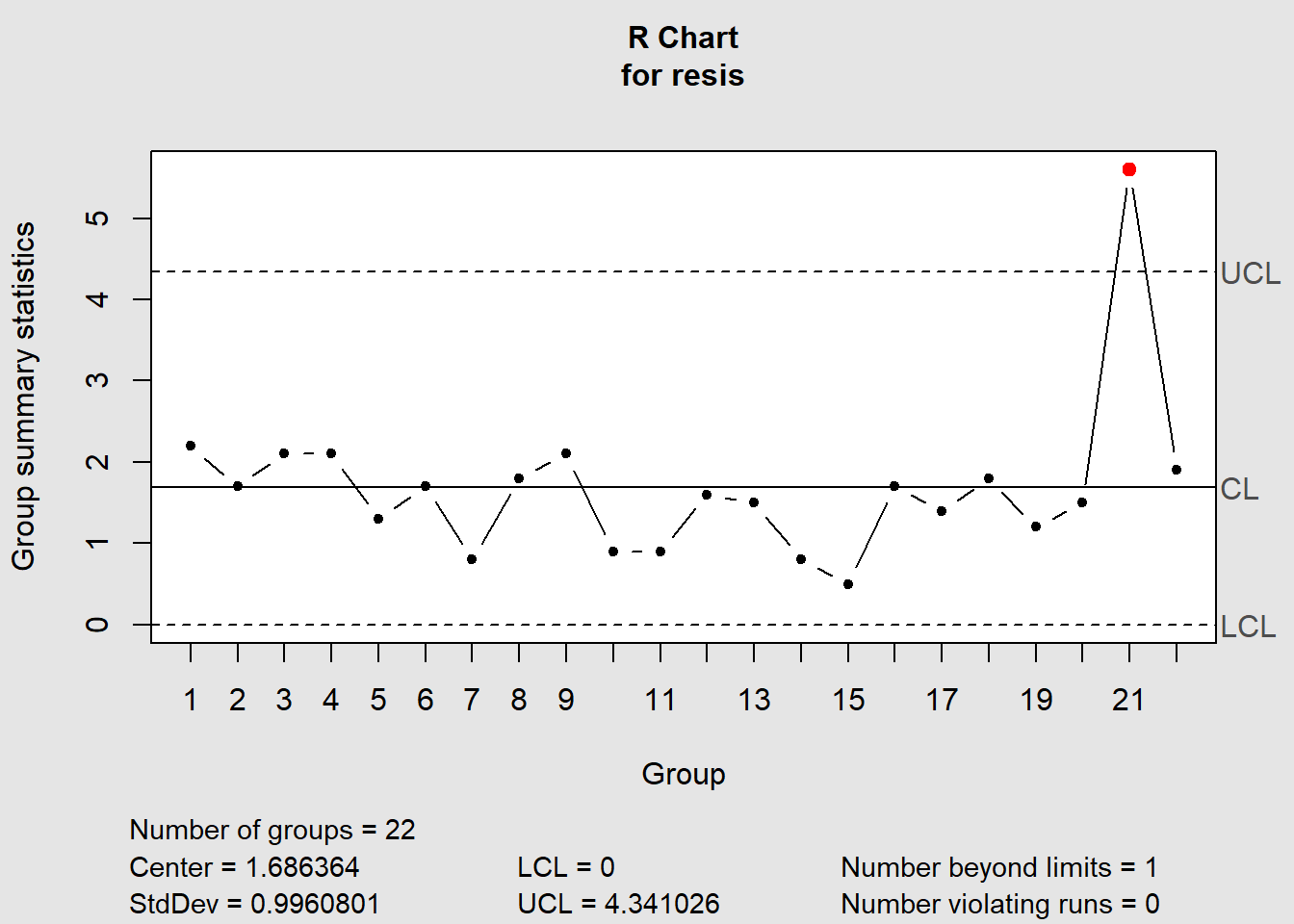
plot(desviospadrao, pch=16, xlab='Dia', ylab='Desvios padrão', ylim=c(0,3),axes=FALSE)
axis(1,at=1:22)#inserindo o eixo x
axis(2)#inserindo o eixo y
abline(h = LCI, col='red')#colocando o LCI
abline(h = LCS, col='red')#colocando o LCS
abline(h = sbarra, col='blue')#colocando a média de controle 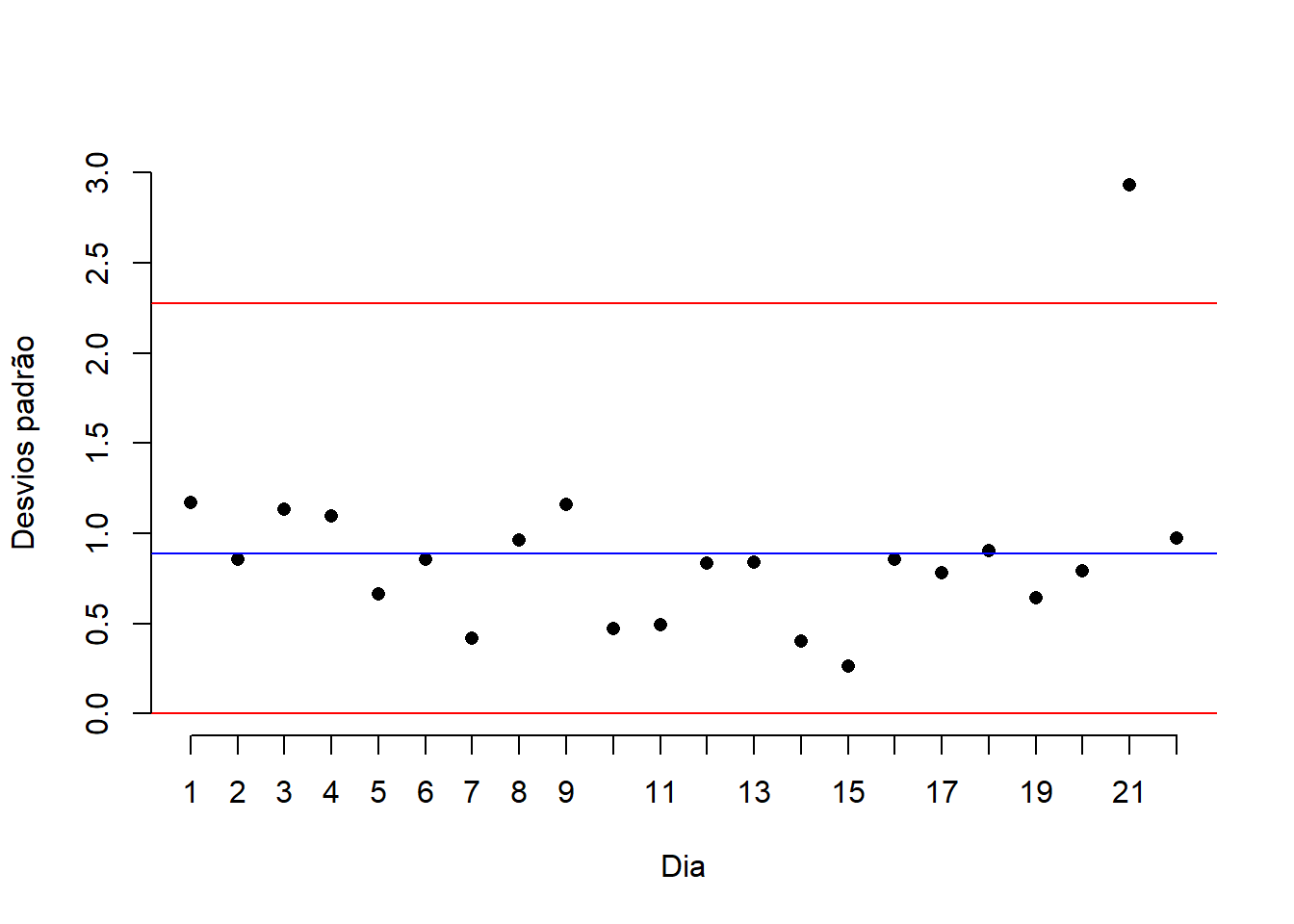
Utilizando o pacote qcc temos,
# colocando os dados de modo que o pacote entenda
resis <- with(ex3, qcc.groups(resistencia, dia))
qs <- qcc(resis, type='S') 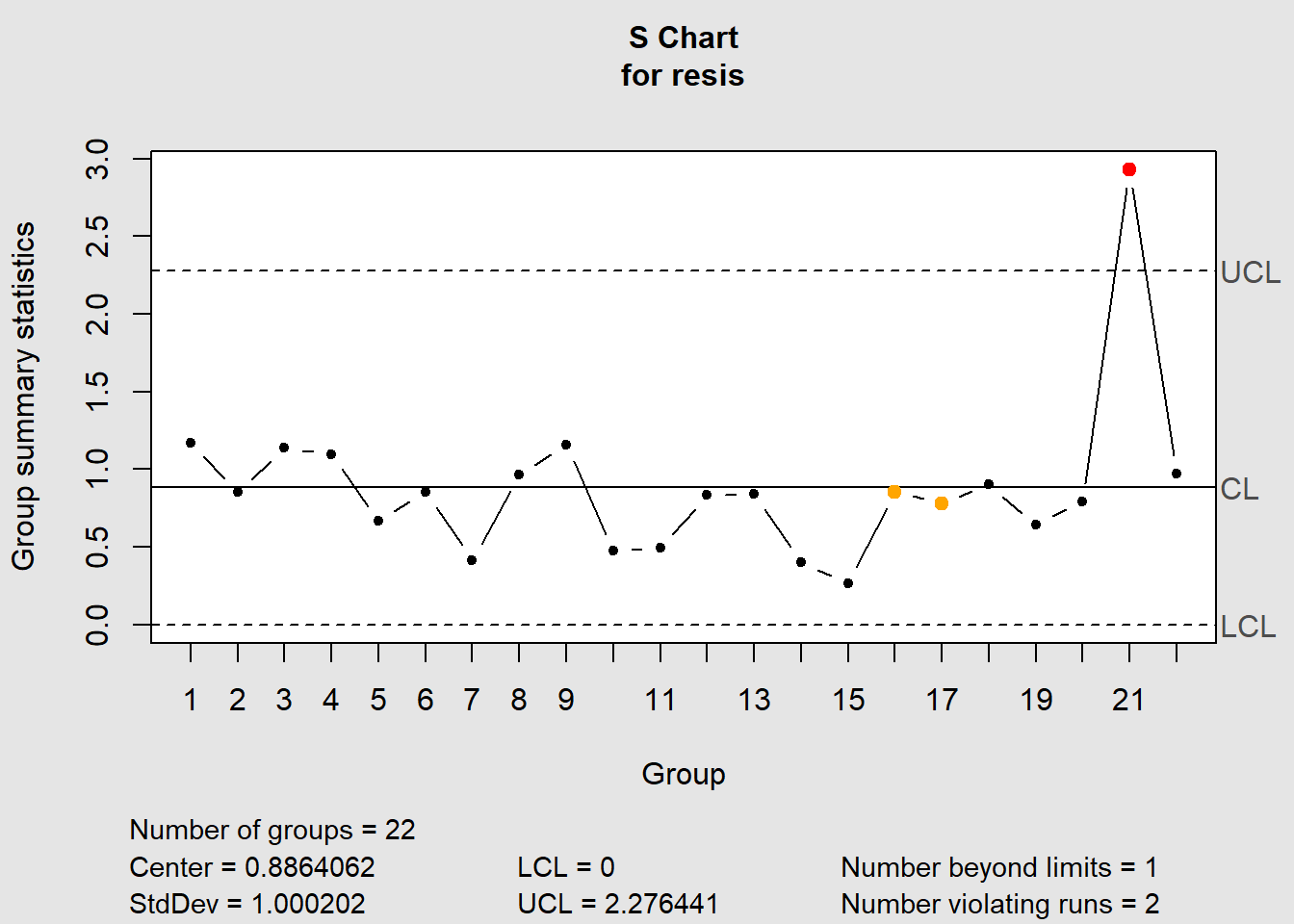
Um ponto ficou fora dos limites calculados indicando que o processo não está sob controle, ou seja, o processo não está estável. Neste momento o responsável pelo gerenciamento de produção deve agir rápido para detectar a causa da instabilização evitando deste modo que o processo seja prejudicado.
6.2 O gráfico R
A letra \(R\) é de amplitude (Range) que é a medida de variabilidade mais simples que tem, pois uma vez que os dados estão ordenados, então a amplitude é o maior valor menos o menor valor conforme já vimos em probabilidade e estatística.
Consideremos que \(r_1, r_2, \cdots, r_t\) são as amplitudes das amostras tomadas no tempo \(t\). Então a média destas amplitudes iremos denotar como \(\bar{r}\). O desvio padrão da amplitude será estimada como \(\hat{\sigma_{R}} = c_{n} \bar{r}/b_{n}\). O valor de \(c_n\) é o desvio padrão da amplitude da amostra aleatória de tamanha \(n\) de uma distribuição normal padronizada. Já \(b_n\) é o valor esperado da amplitude de uma amostra normal padronizada. Para \(n\) variando de 3 a 8 tem-se a seguinte tabela:
tabcn = rbind(n=3:8,cn=c(0.888,0.880,0.864,0.848,0.833,0.820),bn=c(1.693,2.058,2.325,2.536,2.706, 2.844))
knitr::kable(tabcn) Logo podemos calcular os limites da seguinte forma:
\[ LCI = \bar{r} - 3\cdot\hat{\sigma_{R}} \qquad LCS = \bar{r} + 3\cdot\hat{\sigma_{R}} \]
Novamente se \(LCI\) for negativo então utiliza-se \(LCI = 0\).
6.2.1 Aplicação
Utilizando os dados do exemplo anterior faço o gráfico R.
amplitudes = with(ex3, tapply(resistencia,dia,function(x)diff(range(x))))
amplitudes## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
## 2.2 1.7 2.1 2.1 1.3 1.7 0.8 1.8 2.1 0.9 0.9 1.6 1.5 0.8 0.5 1.7 1.4 1.8
## 19 20 21 22
## 1.2 1.5 5.6 1.9rbarra = mean(amplitudes)
rbarra## [1] 1.686364sigmachapeuR = 0.888*rbarra/1.693
sigmachapeuR## [1] 0.8845191LCI = rbarra - 3*sigmachapeuR
LCI #menor que zero## [1] -0.9671938LCI = 0
LCS = rbarra + 3*sigmachapeuR
LCS## [1] 4.339921Fazendo o gráfico,
#plotando o gráfico
plot(amplitudes, pch=16, xlab='Dia', ylab='Amplitudes', ylim=c(0,6),axes=FALSE)
axis(1,at=1:22)#inserindo o eixo x
axis(2)#inserindo o eixo y
abline(h = LCI, col='red')#colocando o LCI
abline(h = LCS, col='red')#colocando o LCS
abline(h = rbarra, col='blue')#colocando a média de controle 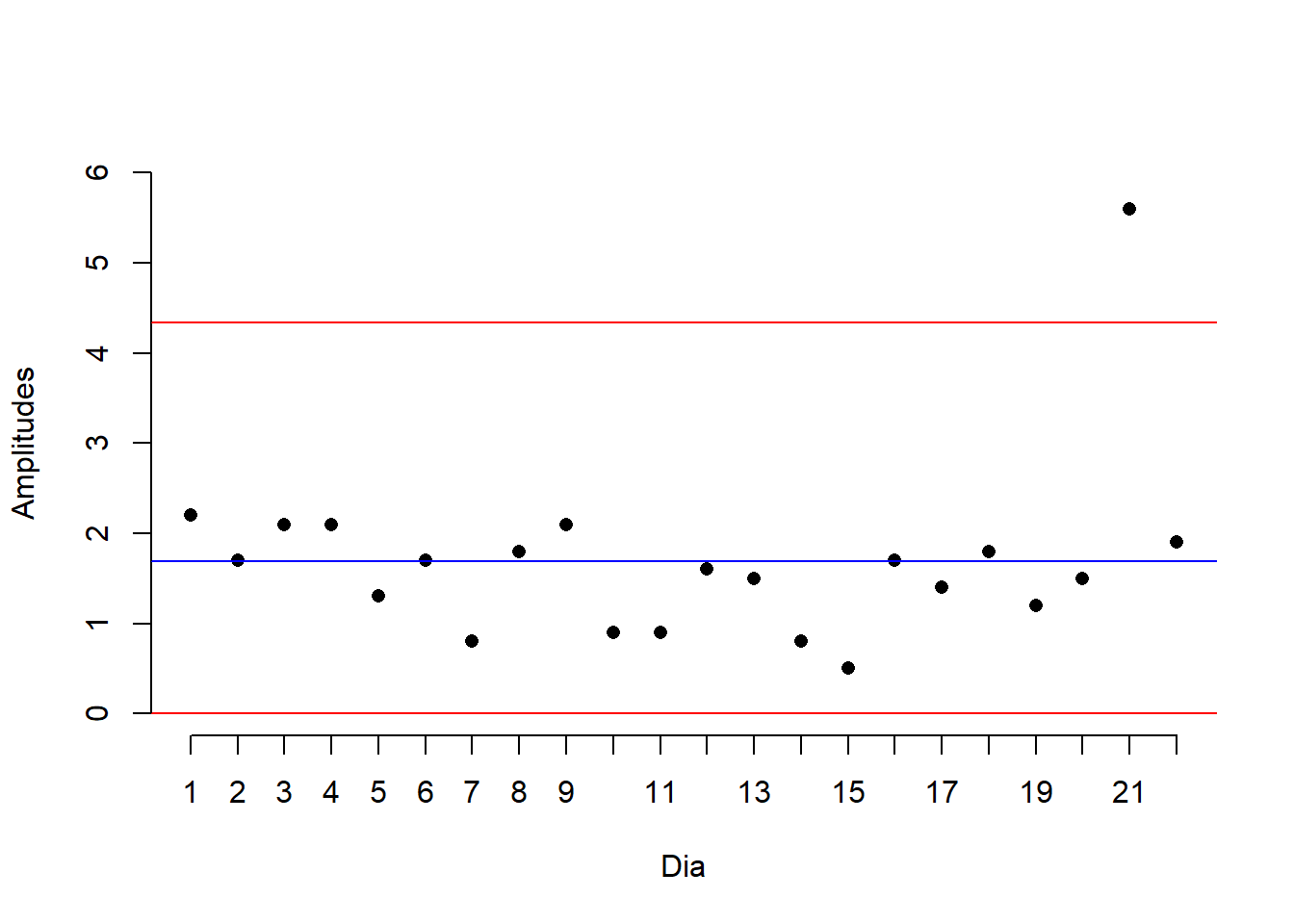
Utilizando o pacote qcc temos,
# colocando os dados de modo que o pacote entenda
qrr = qcc(resis, type='R')